欧陆娱乐數理與統計學院王文濤副教授在國際學術期刊《Fuzzy Sets and Systems》上發表關於帶變系數和比例時滯模糊細胞神經網絡的有限時間同步的最新研究成果。

模糊細胞神經網絡在心理物理學、演講、知覺♠️🖖🏼、機器人、自適應模式識別🖐🏼、視覺和圖像處理等領域有大量應用價值🕌，有關其穩定性🎚、周期性和同步性有很多結果🫑🏃‍♀️。盡管考慮到時滯對模糊細胞神經網絡模型的影響🐳，但是一般都是在常數系數以及有界時滯條件下的結果🆘。在現實世界中，模糊細胞神經網絡模型中的系數函數都不再是常數🈳，而是變化的函數，並且時滯不是有界函數，而是無界的比例時滯。另一方面✌🏼，為了控製時滯模糊細胞神經網絡，有限時間同步是非常有意義的工作，因為它意味著兩個或者多個系統可以在預設的有限時間內達到同步。有限時間同步的結果主要集中在常數系數和有界時滯的神經網絡模型🤰🏽🤦🏿‍♂️，而關於帶變系數和比例時滯模糊細胞神經網絡的有限時間同步還鮮有人涉及🧑🏻。

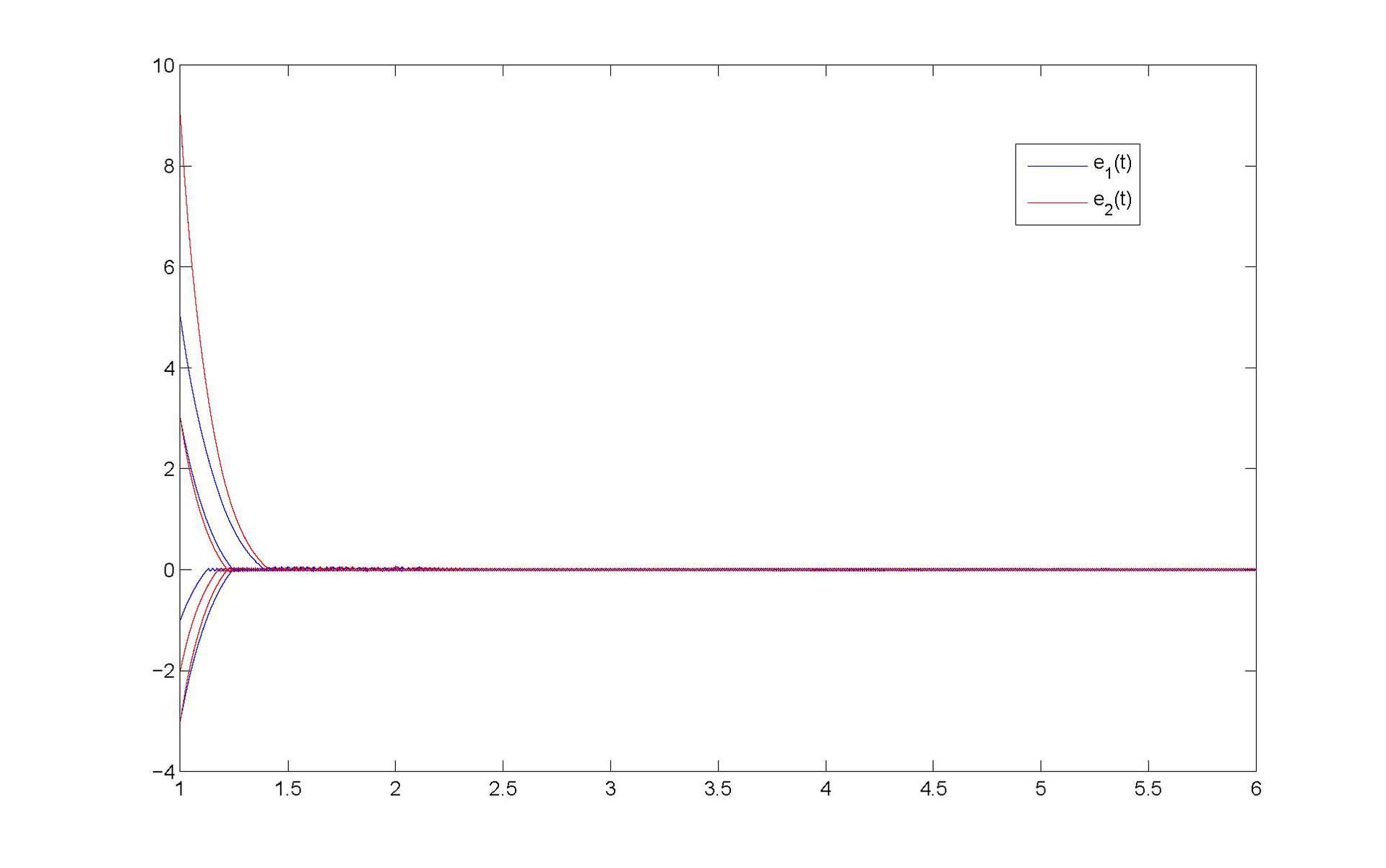
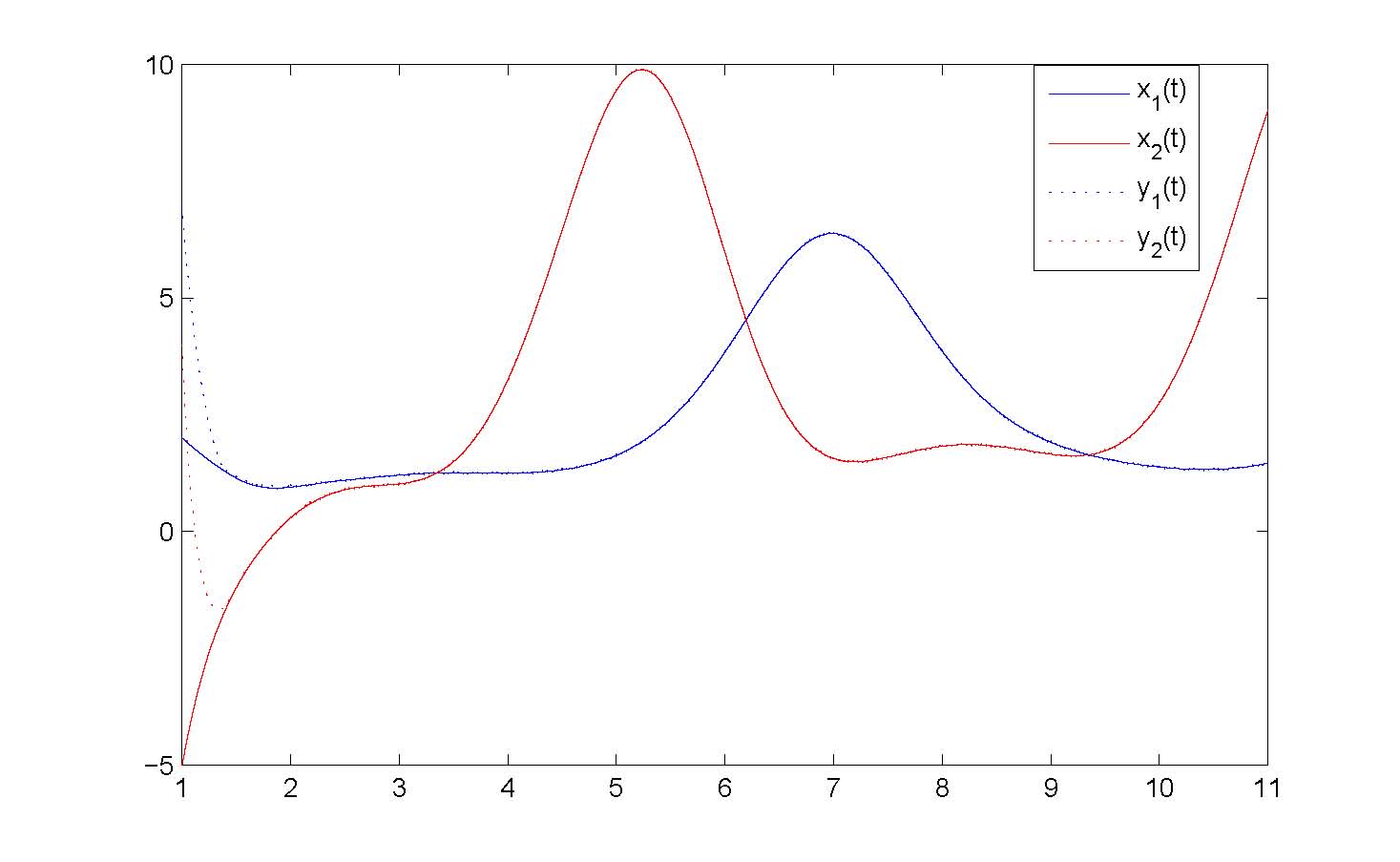
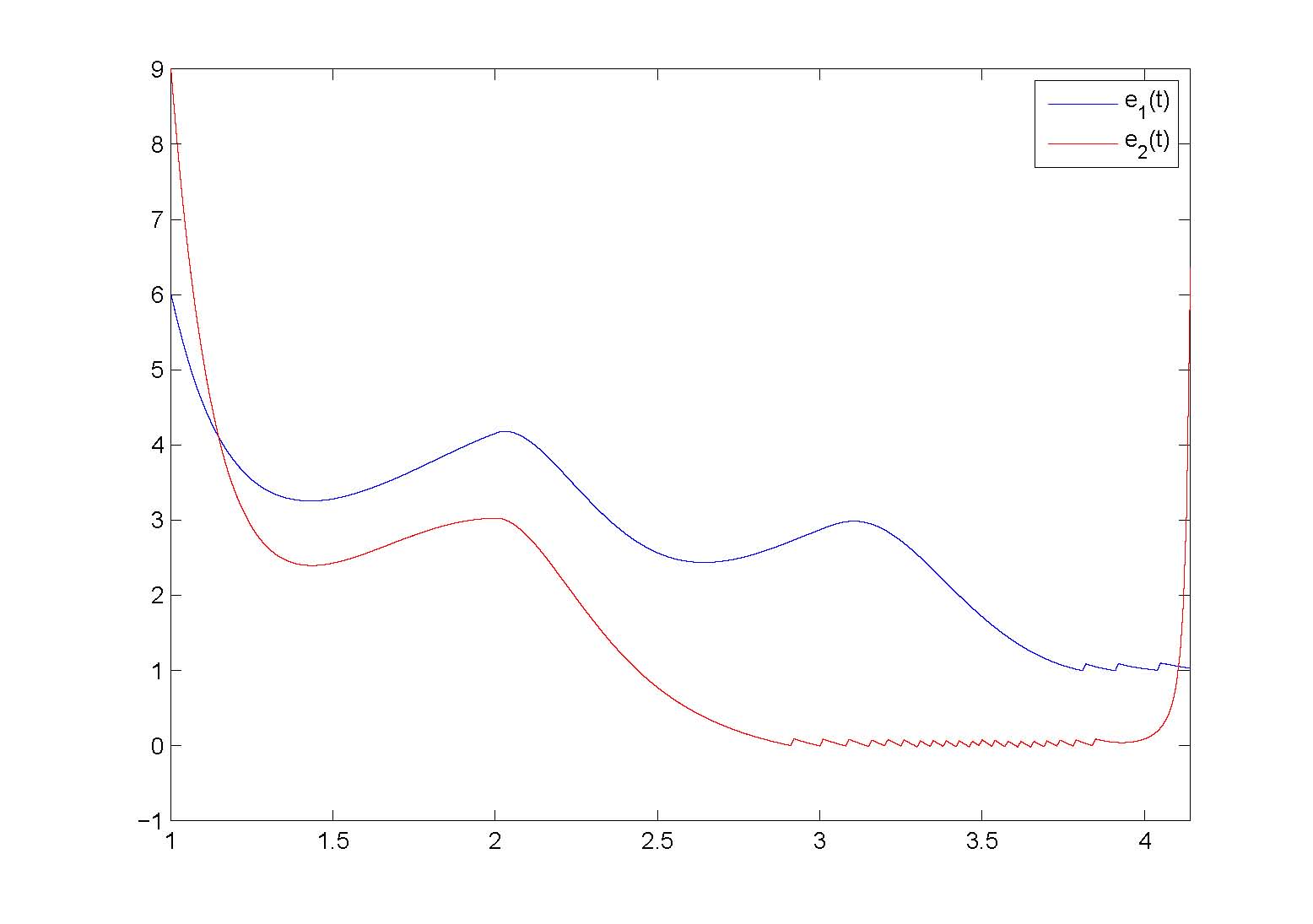
基於有限時間穩定性理論，王文濤副教授應用微分不等式和數學分析技巧，研究了一類帶變系數和比例時滯模糊細胞神經網絡的有限時間同步問題👲🏻，獲得了新的⛎、有效的有限時間同步判斷的充分性條件🏄🏻‍♀️。最後通過一個實例和數值模擬驗證了理論結果的正確性。

該研究成果以“Finite-time synchronization for a class of fuzzy cellular neural networks with time-varying coefficients and proportional delays”為題發表在《Fuzzy Sets and Systems》，主要創新點為👸🏼：（1）考慮的模糊細胞神經網絡模型具有變系數函數和比例時滯🏊‍♀️👉🏻；（2）得到有限時間同步的顯示函數表達式👩‍👩‍👦。《Fuzzy Sets and Systems》為ELSEVIER旗下的知名期刊✍🏼，創刊於1978年🌜，目前影響因子2.718，近5年平均影響因子2.783，是數學🛝、應用數學和計算機領域top期刊